How To Calculate Percentages Easily A Simple Step By Step Guide

Percentages are everywhere—in shopping discounts, tax calculations, exam scores, financial planning, and even nutrition labels. Yet many people hesitate when asked to compute one without a calculator. The truth is, calculating percentages doesn’t require advanced math. With a few foundational techniques, anyone can do it quickly and accurately. This guide breaks down the process into clear, manageable steps, offering practical examples, expert insights, and tools to help you master percentage calculations in daily life.

Understanding What a Percentage Really Means

The word “percent” comes from the Latin *per centum*, meaning “by the hundred.” A percentage expresses a number as a fraction of 100. For example, 25% means 25 out of 100, or 25/100, which simplifies to 0.25 in decimal form. This relationship between percentages, fractions, and decimals is the cornerstone of all percentage calculations.

To convert a percentage to a decimal, divide by 100. So, 40% becomes 0.40. To go the other way—decimal to percentage—multiply by 100. For instance, 0.65 equals 65%. This interchangeability allows flexibility in solving different types of problems.

Tip: Always start by converting the percentage to a decimal before multiplying. It streamlines the calculation and reduces errors.

A Step-by-Step Method for Calculating Percentages

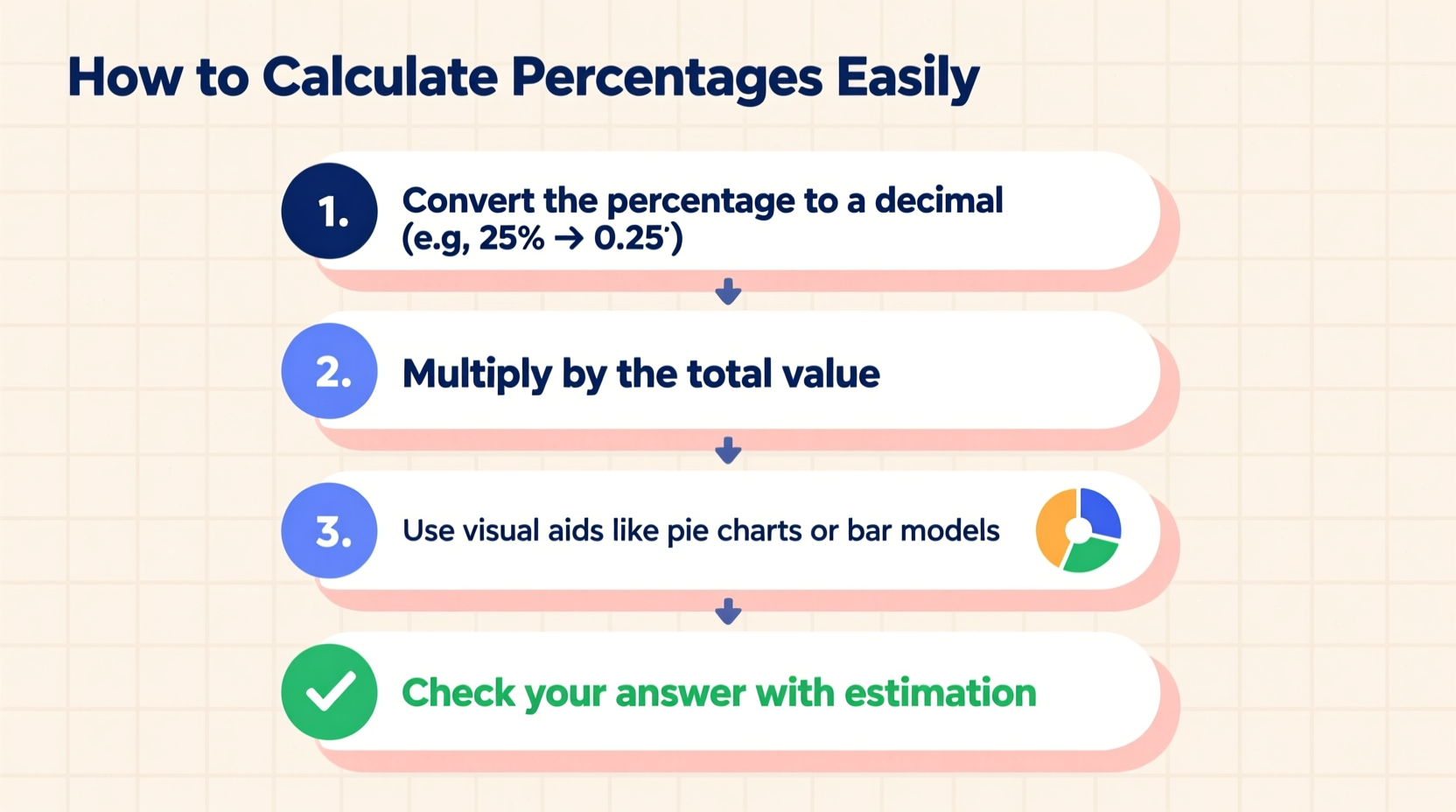
Whether you're figuring out a tip, applying a discount, or analyzing data, follow this universal four-step process:

1. Identify the total amount (the whole). This is your base value—like a bill total, salary, or test score maximum.
2. Determine the portion or rate you're working with. Is it 15% off? A 7% sales tax? Or what percent 35 is of 140?
3. Convert the percentage to a decimal. Move the decimal point two places to the left. For example, 30% → 0.30.
4. Multiply the total by the decimal. This gives you the portion of the whole represented by the percentage.

Example: You want to leave a 20% tip on a $60 meal. Convert 20% to 0.20, then multiply: 60 × 0.20 = 12. The tip is $12.

When You Need to Find What Percent One Number Is of Another

Sometimes, you know two numbers and need to find the percentage relationship between them. For instance, if you scored 42 out of 60 on a test, what percentage did you get?

Use this formula: ( Part ÷ Whole ) × 100 = Percentage

So: (42 ÷ 60) = 0.7 → 0.7 × 100 = 70%. Your score was 70%.

Common Real-Life Applications and Examples

Knowing how to calculate percentages isn’t just academic—it has immediate practical value. Here are three everyday scenarios where these skills come in handy.

1. Shopping Discounts

A jacket is priced at $120 with a 25% discount. How much will you save, and what’s the final price?

• Convert 25% to 0.25.
• Multiply: 120 × 0.25 = 30. You save $30.
• Subtract from original: 120 – 30 = $90 final price.

2. Sales Tax

You buy groceries totaling $85. The local sales tax is 8%. What’s the total cost?

• 8% = 0.08
• 85 × 0.08 = 6.80
• Add to original: 85 + 6.80 = $91.80

3. Salary Increase

Your monthly salary increases from $3,000 to $3,210. What’s the percentage raise?

• Difference: 3,210 – 3,000 = 210
• Divide increase by original: 210 ÷ 3,000 = 0.07
• 0.07 × 100 = 7% raise

“Understanding percentages empowers people to make better financial decisions, from budgeting to investing.” — Dr. Alan Torres, Mathematics Educator and Financial Literacy Advocate

Quick Mental Math Tricks for Faster Calculations

You don’t always need a calculator. These mental shortcuts can help you estimate or compute percentages on the fly.

Percentage	Shortcut Method	Example
10%	Move decimal one place left	10% of 50 → 5.0
5%	Half of 10%	10% of 80 = 8 → 5% = 4
20%	Double 10%	10% of 150 = 15 → 20% = 30
15%	10% + half of 10%	10% of 60 = 6; half = 3 → 6 + 3 = 9
25%	Divide by 4	25% of 80 = 80 ÷ 4 = 20

These tricks are especially useful in restaurants (tipping), retail (discounts), and quick comparisons while budgeting.

Tip: Start with 10%—it’s easy to calculate and serves as a building block for many other percentages.

Common Mistakes and How to Avoid Them

Even simple percentage problems can trip people up due to small but critical errors. Being aware of these pitfalls improves accuracy.

• Mixing up the part and the whole. Always ensure you’re dividing the smaller number by the larger one when finding a percentage.
• Forgetting to convert percentages to decimals. Multiplying 50 × 20% directly leads to errors. Convert 20% to 0.20 first.
• Adding instead of subtracting (or vice versa). When applying a discount, subtract the percentage amount from the original. For taxes or markups, add it.
• Overcomplicating simple cases. Use mental math for common percentages like 10%, 25%, or 50% rather than reaching for a calculator.

Do’s and Don’ts Summary

Do	Don’t
Convert % to decimal before multiplying	Treat % as a whole number in multiplication
Use 10% as a base for estimating	Try to calculate 17% mentally without breaking it down
Double-check whether you need to add or subtract the result	Assume all percentage changes work the same way
Practice with real-world receipts or bills	Rely solely on memory without verifying logic

Mini Case Study: Planning a Home Renovation Budget

Sarah is renovating her kitchen with a $5,000 budget. She allocates 40% to cabinets, 25% to appliances, 20% to labor, and keeps 15% for contingencies. Let’s see how she calculates each portion.

• Cabinets: 40% of 5,000 = 0.40 × 5,000 = $2,000
• Appliances: 25% of 5,000 = 0.25 × 5,000 = $1,250
• Labor: 20% of 5,000 = 0.20 × 5,000 = $1,000
• Contingency: 15% of 5,000 = 0.15 × 5,000 = $750

Total: 2,000 + 1,250 + 1,000 + 750 = $5,000. Her allocation is correct. By using percentages, Sarah ensures proportional spending without exceeding her limit.

FAQ: Common Questions About Percentage Calculations

How do I calculate a percentage increase or decrease?

Subtract the original value from the new value, divide by the original, then multiply by 100. For example, if rent increased from $1,000 to $1,150: (1,150 – 1,000) = 150 → 150 ÷ 1,000 = 0.15 → 15% increase.

Can I use the same method for percentages over 100%?

Absolutely. A 150% increase means the value grows by 1.5 times the original. For instance, 150% of 200 is 200 × 1.5 = 300.

What if I only have the percentage and the result—how do I find the original number?

Use reverse calculation. If 30 is 25% of a number, divide 30 by 0.25. 30 ÷ 0.25 = 120. The original number was 120.

Final Tips for Mastery

• Practice daily: Calculate tips, discounts, or battery percentages mentally.
• Use a consistent formula: Part = Whole × (Percentage as decimal).
• Verify results: Estimate first, then calculate precisely.
• Teach someone else: Explaining reinforces your own understanding.

Conclusion: Take Control of Everyday Math

Calculating percentages is a fundamental skill that enhances decision-making in personal finance, education, and daily choices. By understanding the core principles and practicing regularly, you build confidence and reduce reliance on calculators. These methods are not just for students—they’re essential tools for informed adults navigating a numbers-driven world. Start applying these techniques today, and watch how quickly percentage problems become second nature.

💬 Ready to sharpen your math skills? Try calculating the tip at your next meal or the discount on your online cart—without a calculator. Share your experience or ask questions in the comments!