Mastering How To Multiply Binomials Step By Step Strategies For Easy Algebra Success

Multiplying binomials is a foundational skill in algebra that unlocks the door to factoring, solving quadratic equations, and simplifying complex expressions. While it may seem intimidating at first, breaking down the process into manageable steps transforms it from a confusing chore into a reliable tool. With consistent practice and the right approach, anyone can master this essential technique—regardless of their current math confidence.

The key lies not just in memorizing acronyms like FOIL, but in understanding why each step works and how different methods complement one another. This guide walks through practical strategies, common pitfalls, real-world applications, and expert-backed techniques to ensure lasting comprehension and algebraic fluency.

Understanding Binomials: The Building Blocks

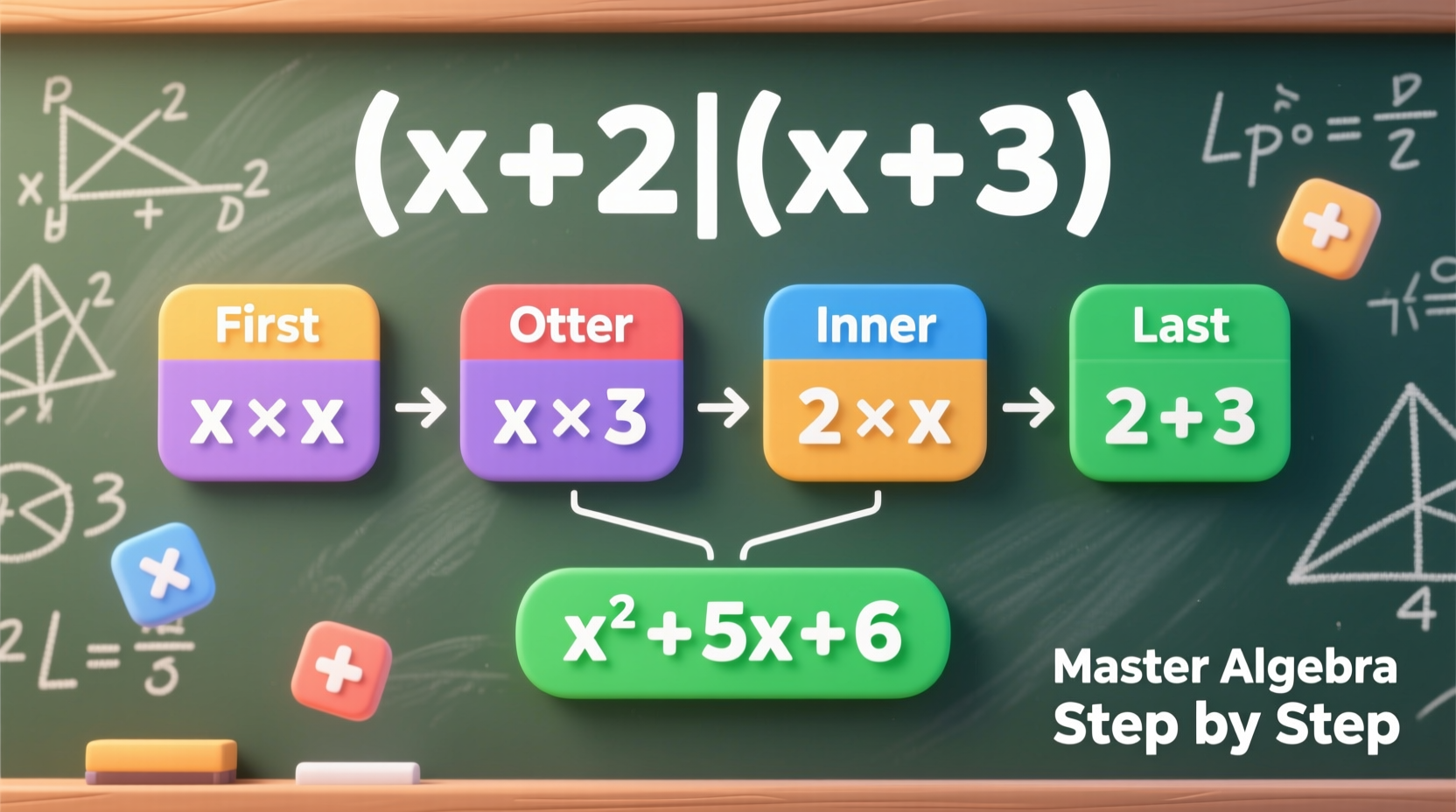
A binomial is an algebraic expression with exactly two terms, such as \\(x + 3\\) or \\(2a - 5b\\). When we multiply two binomials, we are essentially distributing each term in the first binomial across both terms in the second. This operation follows the distributive property: \\(a(b + c) = ab + ac\\), extended to handle two sets of parentheses.

For example, multiplying \\((x + 4)(x + 2)\\) means applying distribution twice—once for \\(x\\) and once for \\(4\\):

1. Distribute \\(x\\) over \\((x + 2)\\): \\(x \\cdot x + x \\cdot 2 = x^2 + 2x\\)
2. Distribute \\(4\\) over \\((x + 2)\\): \\(4 \\cdot x + 4 \\cdot 2 = 4x + 8\\)
3. Add the results: \\(x^2 + 2x + 4x + 8 = x^2 + 6x + 8\\)

This method ensures accuracy even when visual shortcuts aren't immediately clear. It’s also scalable—it works whether you're dealing with variables, coefficients, or negative signs.

Tip: Always write out all intermediate terms before combining like terms. Skipping steps leads to errors, especially with negatives.

Step-by-Step Guide: Mastering the Process

Follow this structured approach to consistently and accurately multiply any pair of binomials.

1. Identify the terms: Label the four components: First, Outer, Inner, Last (FOIL structure).
2. Apply distribution: Multiply each term in the first binomial by each term in the second.
3. Write all products: List every resulting term clearly.
4. Combine like terms: Simplify by adding or subtracting similar variable expressions.
5. Check your work: Plug in a simple value for the variable to verify equivalence.

Let’s apply this to \\((3x - 2)(x + 5)\\):

Step	Action	Result
1	First: \\(3x \\cdot x\\)	\\(3x^2\\)
2	Outer: \\(3x \\cdot 5\\)	\\(15x\\)
3	Inner: \\(-2 \\cdot x\\)	\\(-2x\\)
4	Last: \\(-2 \\cdot 5\\)	\\(-10\\)
5	Combine: \\(3x^2 + 15x - 2x - 10\\)	\\(3x^2 + 13x - 10\\)

The final simplified expression is \\(3x^2 + 13x - 10\\).

Alternative Methods: Beyond FOIL

While FOIL (First, Outer, Inner, Last) is widely taught, it only applies to multiplying two binomials. Relying solely on it can create confusion later when faced with trinomials or higher-order polynomials. A more flexible and powerful strategy is the **area model** (also known as the box method).

In the area model, visualize multiplication as finding the area of a rectangle divided into four smaller sections:

• Label rows with terms from the first binomial.
• Label columns with terms from the second.
• Multiply row and column headers to fill each cell.
• Sum all cells to get the final product.

Using \\((x + 7)(2x - 3)\\):

	\\(2x\\)	\\(-3\\)
\\(x\\)	\\(2x^2\\)	\\(-3x\\)
\\(7\\)	\\(14x\\)	\\(-21\\)

Adding: \\(2x^2 - 3x + 14x - 21 = 2x^2 + 11x - 21\\).

This visual layout reduces sign errors and scales easily to more complex expressions.

“Students who use multiple representations—symbolic, visual, and verbal—develop deeper mathematical understanding.” — Dr. Linda Chen, Mathematics Education Researcher

Common Mistakes and How to Avoid Them

Even strong students stumble on common traps. Recognizing these early prevents frustration and builds confidence.

Common Error	Why It Happens	How to Fix It
Forgetting negative signs	Misreading \\(-5\\) as subtraction rather than a negative term	Treat subtraction as “plus a negative” and distribute carefully
Combining unlike terms	Adding \\(x^2\\) and \\(x\\) as if they were alike	Only combine terms with identical variable powers
Squaring incorrectly: \\((x + 3)^2 = x^2 + 9\\)	Assuming distribution applies linearly to squares	Always expand fully: \\((x+3)(x+3) = x^2 + 6x + 9\\)
Skipping intermediate steps	Trying to do too much mentally	Write every product before simplifying

Tip: Circle or highlight negative terms during distribution to keep track of signs throughout the process.

Real Example: From Homework to Confidence

Jamal, a ninth-grader preparing for his algebra midterm, struggled with multiplying \\((2x - 5)(x + 4)\\). He initially wrote \\(2x^2 + 8x - 5\\), forgetting to distribute \\(-5\\) across both terms. After reviewing his mistake, he began using the area model on scrap paper.

He drew a 2×2 grid, placed \\(2x\\) and \\(-5\\) on the left, and \\(x\\) and \\(4\\) on top. Filling each box helped him see that \\(-5 \\cdot x = -5x\\) and \\(-5 \\cdot 4 = -20\\). Adding all parts gave him \\(2x^2 + 8x - 5x - 20 = 2x^2 + 3x - 20\\).

By checking his answer with \\(x = 1\\):

• Original: \\((2(1) - 5)(1 + 4) = (-3)(5) = -15\\)
• Final expression: \\(2(1)^2 + 3(1) - 20 = 2 + 3 - 20 = -15\\)

The values matched. Jamal now uses the box method on every problem until he feels confident enough to transition back to symbolic manipulation—with far fewer errors.

Checklist: Multiply Binomials Accurately Every Time

Use this checklist before submitting homework or taking a test:

• ☑ Identify all four terms in both binomials
• ☑ Apply distribution to every combination (FOIL or area model)
• ☑ Write all intermediate products—don’t skip steps
• ☑ Pay special attention to negative signs
• ☑ Combine only like terms (same variables and exponents)
• ☑ Verify by substituting a number for the variable
• ☑ Double-check arithmetic and exponents

FAQ: Frequently Asked Questions

Can I use FOIL for any polynomial multiplication?

No. FOIL only works for multiplying two binomials. For trinomials or larger expressions, use the distributive property or the area model instead.

What should I do if there are three binomials?

Multiply two at a time. Start with the first two, simplify the result, then multiply that by the third binomial. Order matters less due to associativity, but neat organization helps avoid mistakes.

Is there a faster way once I understand the basics?

Yes—after mastery, patterns like \\((a + b)^2 = a^2 + 2ab + b^2\\) allow quick expansion. But always derive them first through multiplication to build intuition.

Conclusion: Build Algebraic Fluency One Step at a Time

Multiplying binomials isn’t just a one-off task—it’s a gateway to advanced algebra, calculus, and real-world modeling. Mastery comes not from rote repetition, but from understanding the logic behind each step and practicing with intention. Whether you prefer FOIL, the area model, or pure distribution, consistency and precision matter most.

💬 Ready to strengthen your algebra foundation? Practice one binomial multiplication daily using two different methods. Share your progress or questions in the comments—every expert was once a beginner.