Mastering How To Solve For Arcsin Step By Step Methods And Practical Tips

The inverse sine function, commonly known as arcsin, plays a vital role in trigonometry, calculus, physics, and engineering. Whether you're analyzing waveforms, solving triangles, or working on integrals, understanding how to solve for arcsin accurately is essential. Unlike basic arithmetic, arcsin requires a firm grasp of domain restrictions, unit circle principles, and calculator usage. This guide breaks down the process into clear, actionable steps and equips you with strategies to avoid common pitfalls.

Understanding What Arcsin Really Means

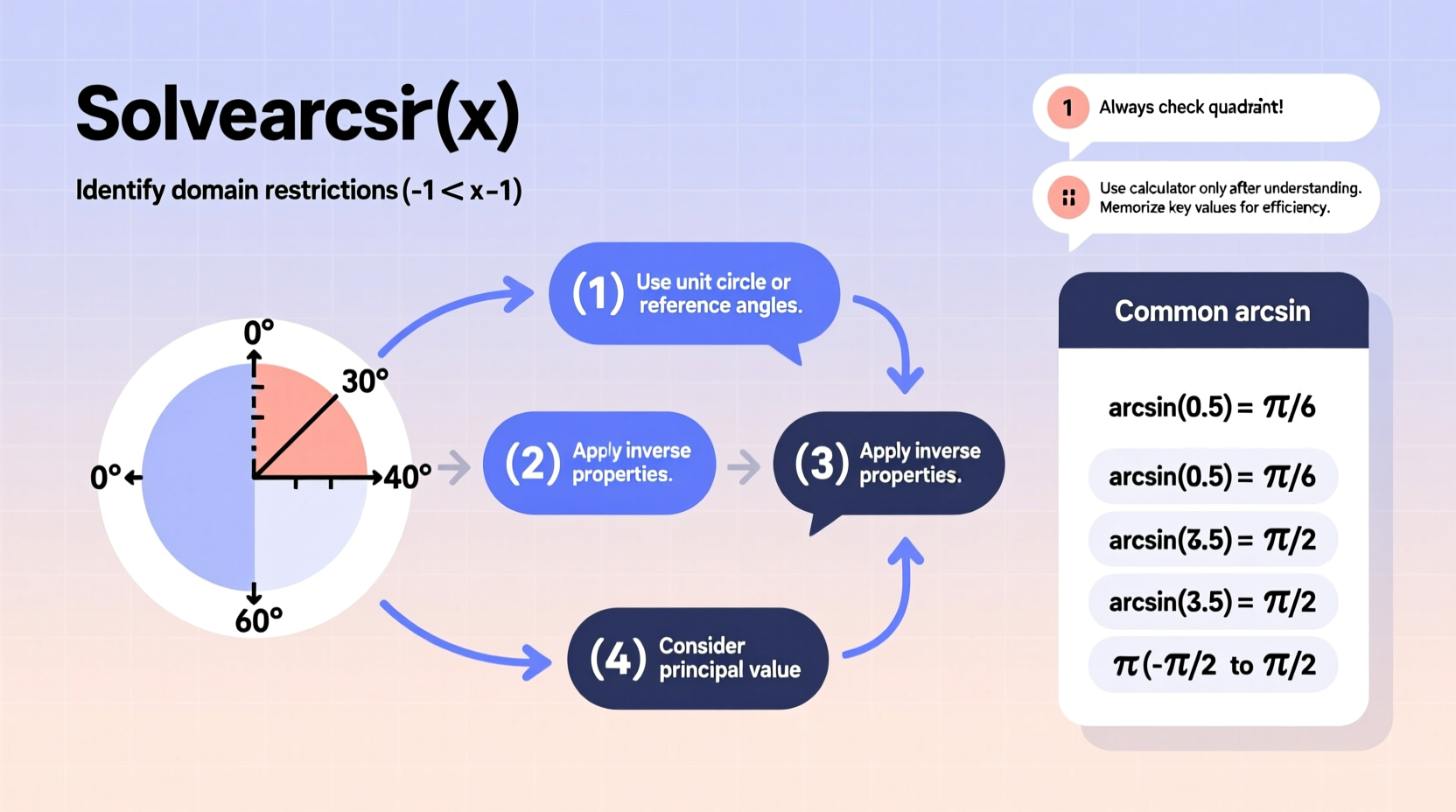
Arcsin, written as \\(\\arcsin(x)\\) or \\(\\sin^{-1}(x)\\), is the inverse of the sine function. It answers the question: “What angle has a sine value of \\(x\\)?” For example, if \\(\\sin(\\theta) = 0.5\\), then \\(\\theta = \\arcsin(0.5)\\). However, unlike regular functions, arcsin is only defined for inputs between -1 and 1, inclusive. This restriction exists because the sine of any angle always falls within that range.

Additionally, arcsin returns values only in the interval \\([- \\frac{\\pi}{2}, \\frac{\\pi}{2}]\\), or \\([-90^\\circ, 90^\\circ]\\) in degrees. This ensures the function remains single-valued — a requirement for inverses. Outside this range, other angles may have the same sine value due to periodicity, but arcsin gives only the principal value.

Tip: Always verify that your input is between -1 and 1. Any value outside this range will result in an undefined arcsin.

Step-by-Step Guide to Solving for Arcsin

Solving for arcsin systematically helps prevent errors and builds confidence. Follow these six steps to find the angle corresponding to a given sine value.

1. Check the domain: Confirm that the input \\(x\\) satisfies \\(-1 \\leq x \\leq 1\\). If not, the expression is undefined.
2. Determine the context: Decide whether the answer should be in radians or degrees based on the problem’s requirements.
3. Use known values from the unit circle: For common values like \\(0, \\pm0.5, \\pm\\frac{\\sqrt{2}}{2}, \\pm\\frac{\\sqrt{3}}{2}, \\pm1\\), recall their corresponding angles.
4. Apply symmetry when needed: If dealing with negative inputs, remember that \\(\\arcsin(-x) = -\\arcsin(x)\\), since sine is odd.
5. Use a calculator (if necessary): For non-standard values, use the \\(\\sin^{-1}\\) button, ensuring the device is set to the correct mode (radians or degrees).
6. Interpret the result: Ensure the output lies within \\([- \\frac{\\pi}{2}, \\frac{\\pi}{2}]\\) for radians or \\([-90^\\circ, 90^\\circ]\\) for degrees.

This method works equally well for symbolic expressions, numerical problems, or real-world applications involving right triangles.

Common Values and Reference Table

Familiarizing yourself with standard arcsin results speeds up problem-solving. The table below lists frequently encountered sine values and their corresponding arcsin outputs.

\\(x\\)	\\(\\arcsin(x)\\) (Degrees)	\\(\\arcsin(x)\\) (Radians)
-1	-90°	\\(-\\frac{\\pi}{2}\\)
\\(-\\frac{\\sqrt{3}}{2}\\)	-60°	\\(-\\frac{\\pi}{3}\\)
\\(-\\frac{\\sqrt{2}}{2}\\)	-45°	\\(-\\frac{\\pi}{4}\\)
-0.5	-30°	\\(-\\frac{\\pi}{6}\\)
0	0°	0
0.5	30°	\\(\\frac{\\pi}{6}\\)
\\(\\frac{\\sqrt{2}}{2}\\)	45°	\\(\\frac{\\pi}{4}\\)
\\(\\frac{\\sqrt{3}}{2}\\)	60°	\\(\\frac{\\pi}{3}\\)
1	90°	\\(\\frac{\\pi}{2}\\)

Memorizing this chart reduces reliance on calculators and improves mental math efficiency.

Practical Tips for Accurate Calculations

Even experienced students make mistakes when evaluating arcsin. These practical tips help maintain accuracy and deepen conceptual understanding.

• Double-check calculator settings: A common error is leaving the calculator in degree mode when radians are required, or vice versa. Always confirm the mode before computing.
• Watch for extraneous solutions: In equations involving trig identities, additional solutions may exist outside the principal range. Use arcsin to find the base solution, then apply periodicity or symmetry to find others.
• Estimate first: Before using a calculator, estimate the expected angle. If \\(\\arcsin(0.7)\\) yields a result near 45°, a display showing 2° or 120° indicates a setting error.
• Understand limitations: Arcsin cannot return angles in quadrants II or III directly. To find angles in those quadrants with the same sine value, use supplementary angle relationships: \\(\\sin(\\theta) = \\sin(180^\\circ - \\theta)\\).

“Students who master arcsin early build stronger foundations for calculus and differential equations.” — Dr. Alan Reyes, Mathematics Educator at MIT

Real Example: Solving a Physics Problem Using Arcsin

Consider a scenario where a drone ascends at an incline. The vertical height gained is 25 meters over a diagonal flight path of 40 meters. What is the angle of elevation?

We use the definition of sine: \\[ \\sin(\\theta) = \\frac{\\text{opposite}}{\\text{hypotenuse}} = \\frac{25}{40} = 0.625 \\] To find \\(\\theta\\), compute: \\[ \\theta = \\arcsin(0.625) \\]

Using a calculator in degree mode: \\[ \\arcsin(0.625) \\approx 38.68^\\circ \\]

The drone climbs at approximately a 38.7° angle. This demonstrates how arcsin translates real-world ratios into interpretable angular measurements.

Tip: In applied problems, label your triangle clearly—identify opposite, adjacent, and hypotenuse—to avoid misapplying trig functions.

Do’s and Don’ts When Working with Arcsin

Do’s	Don’ts
Verify the input is within [-1, 1]	Assume arcsin can return any angle
Use symmetry: \\(\\arcsin(-x) = -\\arcsin(x)\\)	Ignore negative signs in inputs
Set calculator to correct angle mode	Forget to check degree/radian settings
Refer to unit circle for exact values	Rely solely on calculators for simple cases
Round final answers appropriately	Report excessive decimal places without reason

FAQ

Can arcsin return a negative angle?

Yes. Since the range of arcsin includes negative angles from \\(-\\frac{\\pi}{2}\\) to 0 radians (or \\(-90^\\circ\\) to \\(0^\\circ\\)), it returns negative values for negative inputs. For instance, \\(\\arcsin(-0.5) = -30^\\circ\\).

Is arcsin the same as 1/sin(x)?

No. Arcsin is the inverse function of sine, not the reciprocal. The reciprocal of sine is cosecant (\\(\\csc(x)\\)). Confusing \\(\\sin^{-1}(x)\\) with \\(\\frac{1}{\\sin(x)}\\) is a frequent error—note that the \"-1\" denotes inverse, not exponentiation.

How do I solve equations like \\(\\sin(\\theta) = 0.8\\) for all solutions?

First, find the principal solution: \\(\\theta = \\arcsin(0.8) \\approx 53.13^\\circ\\). Then, use symmetry: another solution exists in Quadrant II: \\(180^\\circ - 53.13^\\circ = 126.87^\\circ\\). Add multiples of \\(360^\\circ\\) (or \\(2\\pi\\)) to both for all general solutions.

Final Thoughts and Call to Action

Mastering arcsin is more than memorizing buttons on a calculator—it’s about understanding the relationship between ratios and angles, recognizing domain constraints, and applying logic across mathematical contexts. With practice, solving for arcsin becomes intuitive, opening doors to advanced topics in science and engineering. Start by drilling common values, then progress to word problems and identities. Share your progress, challenge misconceptions, and test your skills regularly.

💬 Ready to improve your trig fluency? Try solving five arcsin problems today—without a calculator first—and compare your estimates with actual results. Share your experience in the comments!