Interval notation is a compact and precise way to represent sets of real numbers between two endpoints. While it may seem abstract at first, mastering interval notation unlocks clarity in algebra, calculus, and beyond. Whether you're analyzing functions, solving inequalities, or interpreting data ranges, understanding how to write and interpret intervals correctly is essential. This guide breaks down the fundamentals, common pitfalls, and practical applications so you can use interval notation with confidence.
What Is Interval Notation?
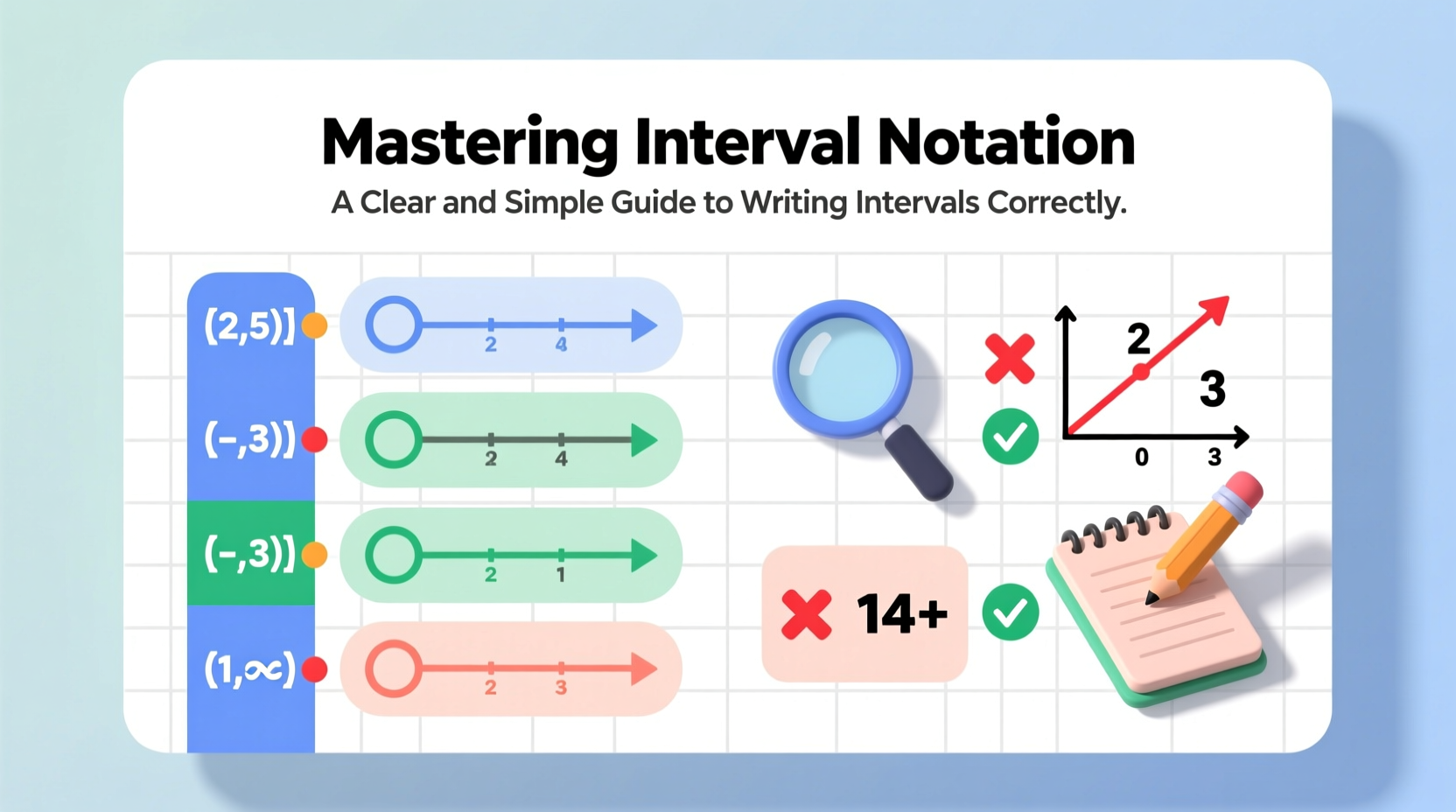
Interval notation describes continuous segments of the real number line. Instead of listing every number in a range—which would be impossible for infinite sets—interval notation uses parentheses and brackets to define boundaries. For example, instead of saying “all numbers greater than 2 and less than or equal to 7,” we write (2, 7]. This concise format reduces ambiguity and streamlines mathematical communication.
The key symbols used are:
- ( ) – Parentheses indicate an open endpoint (not included)
- [ ] – Brackets indicate a closed endpoint (included)
- ∞ or -∞ – Used for unbounded intervals; always paired with parentheses
Types of Intervals and How to Write Them
There are four main types of bounded intervals, each defined by whether the endpoints are included:
| Type | In Words | Interval Notation | Inequality Equivalent |
|---|---|---|---|
| Closed Interval | All numbers from a to b, including both | [a, b] | a ≤ x ≤ b |
| Open Interval | All numbers between a and b, excluding both | (a, b) | a < x < b |
| Half-Open (Left-Closed) | Includes a, excludes b | [a, b) | a ≤ x < b |
| Half-Open (Right-Closed) | Excludes a, includes b | (a, b] | a < x ≤ b |
For intervals that extend infinitely in one direction, we use ∞ or -∞ with parentheses only. For instance:
- [3, ∞) means all numbers greater than or equal to 3
- (-∞, 0) means all negative numbers
- (-∞, ∞) represents the entire real number line
Step-by-Step Guide to Writing Correct Interval Notation
Follow these steps to accurately convert verbal descriptions or inequalities into proper interval notation:
- Identify the lower and upper bounds. Determine the smallest and largest values in the set. If no bound exists, use -∞ or ∞ accordingly.
- Determine inclusion of endpoints. Check if the inequality uses ≤ or ≥ (include endpoint → bracket) or < or > (exclude endpoint → parenthesis).
- Write the left endpoint first. Always list the smaller number on the left, even if it's -∞.
- Use correct symbols. Open endpoints get parentheses; closed ones get brackets.
- Verify continuity. Ensure there are no gaps unless dealing with unions (see below).
For compound conditions like “x < -2 or x ≥ 5,” combine intervals using the union symbol (∪): (-∞, -2) ∪ [5, ∞).
Common Mistakes and How to Avoid Them
Even experienced students make errors when learning interval notation. Here are frequent missteps and corrections:
| Mistake | Why It’s Wrong | Correct Version |
|---|---|---|
| [3, -1] | Lower bound must come first | [-1, 3] |
| (4, ∞] | Infinity is never included; always use ( | (4, ∞) |
| -2 < x ≤ 5 written as [-2, 5) | Misaligned symbols due to incorrect interpretation | (-2, 5] |
| {x | x ≠ 0} written as (-∞, 0), (0, ∞) | Comma doesn’t denote union in formal notation | (-∞, 0) ∪ (0, ∞) |
“Precision in notation reflects precision in thinking. A misplaced bracket can change the meaning of a solution set entirely.” — Dr. Alan Reyes, Mathematics Educator and Curriculum Developer
Real-World Example: Modeling Temperature Ranges
Consider a refrigerated storage unit designed to keep food safe. The ideal temperature range is above 34°F but no higher than 40°F. Using inequality notation: 34 < T ≤ 40.
In interval notation, this becomes (34, 40]. The open parenthesis at 34 indicates that exactly 34°F is not acceptable (risk of freezing), while the bracket at 40 means 40°F is allowed but should not be exceeded.
If engineers were to miswrite this as [34, 40], they’d incorrectly allow temperatures at or below 34°F, potentially damaging sensitive products. Proper interval notation prevents such costly misunderstandings in technical documentation and control systems.
Checklist: Writing Accurate Interval Notation
Before finalizing your interval, run through this checklist:
- ✅ Are the endpoints listed in ascending order?
- ✅ Are parentheses used for excluded values?
- ✅ Are brackets used for included values?
- ✅ Is infinity always paired with a parenthesis?
- ✅ Are disjoint sets joined with ∪, not commas?
- ✅ Does the interval match the original inequality or condition?
Frequently Asked Questions
Can an interval be a single point?
Yes. A single number like x = 5 can be written as the closed interval [5, 5]. Though uncommon, it’s mathematically valid and sometimes used in set theory or optimization problems.
Is zero included in (-3, 3)?
Yes. Since -3 < 0 < 3, zero lies strictly within the open interval (-3, 3) and is therefore included, despite neither endpoint being part of the set.
How do I write all real numbers except 1?
You would express this as the union of two intervals: (-∞, 1) ∪ (1, ∞). This shows all numbers less than 1 and all numbers greater than 1, excluding 1 itself.
Conclusion: Apply Your Knowledge with Confidence
Interval notation is more than just a symbolic shorthand—it’s a foundational tool for expressing continuity, domain, range, and constraints across mathematics and applied sciences. By understanding its logic and practicing consistent formatting, you eliminate ambiguity and enhance your problem-solving accuracy. Whether you’re graphing functions, solving compound inequalities, or modeling real-world thresholds, precise interval notation ensures your ideas are communicated clearly and correctly.









 浙公网安备
33010002000092号
浙公网安备
33010002000092号 浙B2-20120091-4
浙B2-20120091-4
Comments
No comments yet. Why don't you start the discussion?