Simple And Effective Methods To Calculate The Height Of Any Prism

Understanding how to determine the height of a prism is essential in geometry, architecture, engineering, and everyday problem-solving. Whether you're working with triangular, rectangular, or pentagonal prisms, knowing the correct method to find height ensures accuracy in design, construction, and academic work. Unlike width or length, height isn't always labeled—especially in irregular or complex shapes. This guide breaks down practical, reliable techniques to calculate the height of any prism, no matter its base shape or available data.

What Is a Prism and Why Height Matters

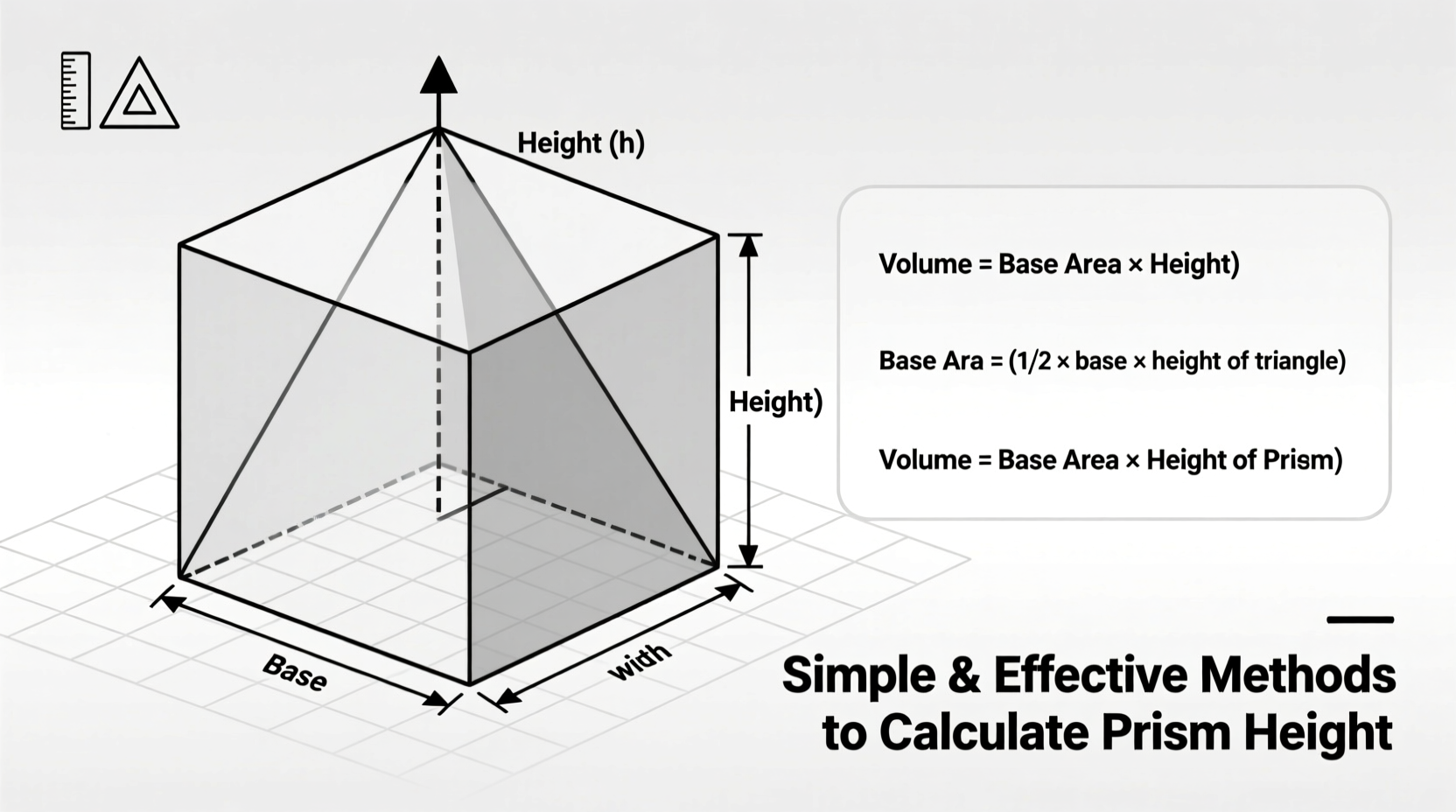
A prism is a three-dimensional solid with two parallel, congruent bases connected by lateral faces that are parallelograms. The height of a prism refers to the perpendicular distance between these two bases. It's crucial to distinguish this from slant height or edge length, which may appear similar but serve different purposes.

The height plays a central role in calculating volume and surface area. For example, the formula for volume is:

Volume = Base Area × Height

If you know the volume and the base area, you can rearrange this equation to solve for height. But what if only partial information is given? That’s where multiple calculation strategies come into play.

Step-by-Step: Calculating Height Using Volume and Base Area

This is the most straightforward method when both volume and base area are known. Follow these steps:

1. Determine the volume of the prism (usually provided or measured).
2. Calculate the area of the base. This depends on the base shape:
   • Rectangle: length × width
   • Triangle: (base × height) / 2
   • Regular polygon: use appropriate area formulas (e.g., for hexagons)
3. Rearrange the volume formula: Height = Volume ÷ Base Area.
4. Perform the division to get the height.

Tip: Always ensure units match. If volume is in cm³ and base area in cm², height will be in cm.

Real Example: Finding the Height of a Chocolate Box

Imagine a chocolate manufacturer produces boxes shaped like rectangular prisms. One box has a volume of 480 cm³, with a base measuring 8 cm by 6 cm. To find the height:

Base Area = 8 × 6 = 48 cm²
Height = 480 ÷ 48 = 10 cm

The box is 10 cm tall. This helps in stacking, packaging, and shelf design.

Using Lateral Edge and Angle (For Right Prisms)

In some cases, especially with right prisms, you might not have volume data but do know the angle between the lateral edge and the base. In such scenarios, trigonometry becomes useful.

If the lateral edge (the side connecting the two bases) is inclined at an angle θ to the base, then:

Height = Lateral Edge Length × sin(θ)

This method applies primarily to oblique prisms where the sides aren’t perpendicular to the base. For right prisms, the lateral edges are already perpendicular, so the height equals the edge length directly.

Mini Case Study: Architectural Modeling

An architect designs a glass atrium shaped like a hexagonal prism. The structure uses diagonal support beams forming a 75° angle with the ground. Each beam is 6 meters long. To compute vertical clearance inside:

Height = 6 × sin(75°) ≈ 6 × 0.9659 ≈ 5.8 meters

This confirms sufficient headroom for foot traffic and lighting fixtures.

Applying the Pythagorean Theorem in Composite Problems

When dealing with prisms embedded within other shapes or when only diagonal measurements are available, the Pythagorean theorem can extract height indirectly.

Suppose a rectangular prism has a space diagonal (from one corner to the opposite top corner) of 13 cm. Its length and width are 3 cm and 4 cm respectively. You can find height as follows:

Space diagonal formula: d² = l² + w² + h²
13² = 3² + 4² + h²
169 = 9 + 16 + h² → h² = 144 → h = 12 cm

This approach is valuable in spatial reasoning problems and 3D modeling software troubleshooting.

Method	Required Information	Best For
Volume & Base Area	Volume, base dimensions	Standard prisms with known volume
Trigonometry	Lateral edge, angle to base	Oblique prisms
Pythagorean Theorem	Diagonals, length/width	Spatial puzzles, missing height
Similar Triangles	Proportional models or cross-sections	Scaled blueprints, indirect measurement

Expert Insight: When Theory Meets Practice

“Students often memorize formulas without visualizing the prism. I always recommend sketching the base and labeling all known values first. That mental model makes choosing the right height method intuitive.” — Dr. Alan Reyes, Mathematics Educator and STEM Curriculum Developer

Dr. Reyes emphasizes foundational understanding over rote learning. His students consistently outperform peers on applied geometry tasks because they learn to assess context before selecting a solution path.

Common Mistakes and How to Avoid Them

• Confusing height with slant height: In non-right prisms, edges may look vertical but aren’t truly perpendicular. Always verify alignment.
• Mixing units: Never divide cubic inches by square centimeters. Convert everything first.
• Assuming all prisms are rectangular: Triangular and trapezoidal prisms require correct base area calculations.
• Ignoring significant figures: Maintain precision throughout calculations to avoid rounding errors.

Tip: Double-check whether your prism is right or oblique. This determines whether side length equals height.

Checklist: How to Accurately Calculate Prism Height

Follow this checklist to ensure accuracy every time:

1. ✅ Identify the type of prism (rectangular, triangular, etc.).
2. ✅ Determine if it’s a right or oblique prism.
3. ✅ Measure or obtain the base area using correct geometric formulas.
4. ✅ Confirm whether volume, diagonal, or angular data is available.
5. ✅ Select the appropriate method based on available information.
6. ✅ Perform unit conversions if necessary.
7. ✅ Solve step by step, showing all work for verification.
8. ✅ Verify result by plugging back into volume or diagonal formula.

Frequently Asked Questions

Can you find the height of a prism without knowing the volume?

Yes. If you have the space diagonal and base dimensions, use the Pythagorean theorem. Alternatively, if the prism is part of a larger figure, proportional reasoning or trigonometry may apply.

Does the base shape affect how I calculate height?

The base shape affects how you calculate the base area, but not the height directly. Once base area is known, height derivation remains consistent across prism types using the volume formula.

Is the height always vertical?

Not necessarily. Height is defined as the perpendicular distance between bases, regardless of orientation. Even if a prism lies on its side, the “height” still refers to the shortest line segment joining the two bases at right angles.

Conclusion: Mastering Prism Height Builds Stronger Math Skills

Calculating the height of a prism isn’t just about solving textbook problems—it’s a skill that supports real-world decision-making in design, manufacturing, and planning. By mastering multiple methods—volume-based, trigonometric, and geometric—you gain flexibility and confidence in handling diverse challenges. Whether you're a student preparing for exams or a professional verifying structural dimensions, these techniques provide clarity and precision.

🚀 Ready to apply these methods? Grab a ruler, pick a household object shaped like a prism, and try calculating its height using volume or diagonals. Share your results or questions in the comments below!