Step By Step Methods To Accurately Find The Point Of Intersection Of Two Lines

Finding where two lines meet is a fundamental skill in algebra, geometry, and real-world applications like engineering, computer graphics, and navigation. Whether you're solving a system of equations or mapping out routes on a coordinate plane, knowing how to determine the exact point of intersection ensures precision and clarity. This guide walks through multiple reliable methods—algebraic, graphical, and matrix-based—with practical examples and expert insights to help you master this essential concept.

Understanding the Point of Intersection

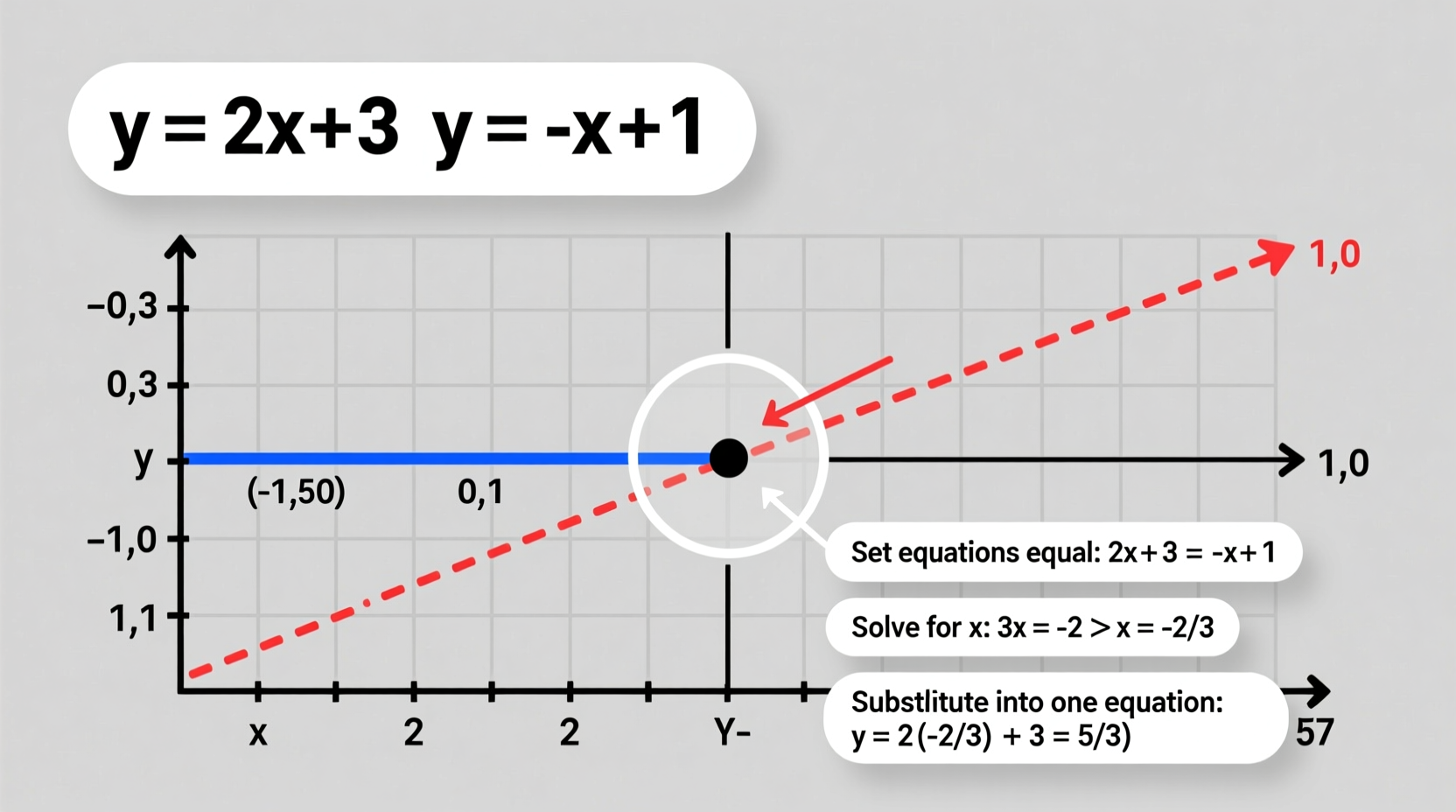
The point of intersection of two lines is the single coordinate (x, y) that satisfies both line equations simultaneously. If two lines are not parallel, they will intersect at exactly one point. If they are parallel and distinct, they never intersect. If they are coincident (the same line), they intersect at infinitely many points.

To determine whether lines intersect and where, you must analyze their slopes and intercepts. Two non-vertical lines with different slopes will always intersect at one unique point.

“Intersection problems form the backbone of linear systems analysis. Mastering them unlocks deeper understanding in calculus, physics, and data science.” — Dr. Alan Reyes, Mathematics Professor at MIT

Method 1: Algebraic Solution Using Substitution

This method works well when one equation is easily solvable for one variable. It involves substituting an expression from one equation into the other to reduce the system to a single-variable equation.

Step-by-step process:

1. Write both line equations in slope-intercept form: \\( y = mx + b \\).
2. Solve one equation for \\( y \\) (if not already done).
3. Substitute the expression for \\( y \\) from the first equation into the second.
4. Solve the resulting equation for \\( x \\).
5. Plug the value of \\( x \\) back into either original equation to find \\( y \\).
6. Write the solution as an ordered pair \\( (x, y) \\).

Example:
Line 1: \\( y = 2x + 3 \\)
Line 2: \\( y = -x + 9 \\)

Set equations equal:
\\( 2x + 3 = -x + 9 \\)
Add \\( x \\) to both sides: \\( 3x + 3 = 9 \\)
Subtract 3: \\( 3x = 6 \\)
Divide by 3: \\( x = 2 \\)

Substitute into Line 1: \\( y = 2(2) + 3 = 7 \\)
Intersection point: \\( (2, 7) \\)

Tip: Always verify your solution by plugging the coordinates into both original equations to ensure they hold true.

Method 2: Elimination Technique

The elimination method is ideal when both equations are in standard form (\\( Ax + By = C \\)). The goal is to eliminate one variable by adding or subtracting the equations after appropriate scaling.

Procedure:

1. Align both equations in standard form.
2. Multiply one or both equations so that the coefficients of one variable are opposites.
3. Add the equations to eliminate one variable.
4. Solve for the remaining variable.
5. Substitute back to find the other variable.
6. Express the result as \\( (x, y) \\).

Example:
Equation 1: \\( 3x + 2y = 12 \\)
Equation 2: \\( 2x - y = 1 \\)

Multiply Equation 2 by 2: \\( 4x - 2y = 2 \\)
Now add to Equation 1:
\\( 3x + 2y + 4x - 2y = 12 + 2 \\)
\\( 7x = 14 \\Rightarrow x = 2 \\)

Substitute into Equation 2: \\( 2(2) - y = 1 \\Rightarrow 4 - y = 1 \\Rightarrow y = 3 \\)
Intersection point: \\( (2, 3) \\)

Method	Best For	When to Avoid
Substitution	One equation already solved for a variable	Complex expressions that make substitution messy
Elimination	Equations in standard form	When coefficient alignment requires large multipliers
Graphical	Quick visual estimation	Precision-critical tasks
Matrix (Cramer’s Rule)	Systems with consistent structure	Non-linear or higher-dimension systems without determinants

Method 3: Graphical Estimation

While less precise than algebraic methods, graphing provides a visual understanding of how and where lines intersect. This approach is useful for checking solutions or gaining intuition about a problem.

Steps:

• Plot both lines on the same coordinate plane.
• Identify the point where the lines cross.
• Read off the approximate coordinates.

For accuracy, use graph paper or digital tools like Desmos or GeoGebra. While manual plotting may introduce human error, software renders exact intersections based on input equations.

Tip: Use graphing calculators or online tools to confirm algebraic results—visual verification builds confidence in your answers.

Method 4: Matrix Method Using Cramer’s Rule

For advanced learners or those working within linear algebra frameworks, Cramer’s Rule offers an elegant way to solve 2×2 systems using determinants.

Given two equations: \\[ a_1x + b_1y = c_1 \\\\ a_2x + b_2y = c_2 \\] The solution is: \\[ x = \\frac{ \\begin{vmatrix} c_1 & b_1 \\\\ c_2 & b_2 \\end{vmatrix} }{ \\begin{vmatrix} a_1 & b_1 \\\\ a_2 & b_2 \\end{vmatrix} }, \\quad y = \\frac{ \\begin{vmatrix} a_1 & c_1 \\\\ a_2 & c_2 \\end{vmatrix} }{ \\begin{vmatrix} a_1 & b_1 \\\\ a_2 & b_2 \\end{vmatrix} } \\] provided the denominator (determinant) is not zero.

Example:
\\( 2x + 3y = 7 \\)
\\( 4x - y = 1 \\)

Determinant: \\( D = (2)(-1) - (3)(4) = -2 - 12 = -14 \\)

\\( D_x = \\begin{vmatrix}7 & 3 \\\\ 1 & -1\\end{vmatrix} = (7)(-1) - (3)(1) = -7 - 3 = -10 \\)
\\( D_y = \\begin{vmatrix}2 & 7 \\\\ 4 & 1\\end{vmatrix} = (2)(1) - (7)(4) = 2 - 28 = -26 \\)

\\( x = \\frac{-10}{-14} = \\frac{5}{7}, \\quad y = \\frac{-26}{-14} = \\frac{13}{7} \\)
Intersection: \\( \\left(\\frac{5}{7}, \\frac{13}{7}\\right) \\)

Mini Case Study: Urban Planning Application

In city planning, engineers often model pedestrian pathways as linear equations to predict foot traffic intersections. Suppose two walkways are represented by:

Path A: \\( y = 0.5x + 2 \\)
Path B: \\( y = -1.5x + 10 \\)

Using substitution:
\\( 0.5x + 2 = -1.5x + 10 \\)
\\( 2x = 8 \\Rightarrow x = 4 \\)
Then \\( y = 0.5(4) + 2 = 4 \\)

The paths intersect at (4, 4). Planners place a water fountain here, maximizing accessibility. Accurate calculation prevents misplacement and improves user experience.

Checklist: How to Accurately Find Intersections

• ✅ Confirm the lines are not parallel by comparing slopes.
• ✅ Rewrite equations in consistent form (slope-intercept or standard).
• ✅ Choose the most efficient method based on equation format.
• ✅ Solve for one variable, then substitute to find the other.
• ✅ Verify the solution in both original equations.
• ✅ Use graphing tools to visually confirm the result.
• ✅ Express the final answer as an ordered pair \\( (x, y) \\).

FAQ

What if the lines are parallel?

If two lines have the same slope but different y-intercepts, they are parallel and do not intersect. If they have the same slope and intercept, they are the same line and intersect at all points.

Can vertical lines intersect horizontal ones?

Yes. A vertical line (e.g., \\( x = 3 \\)) and a horizontal line (e.g., \\( y = 5 \\)) intersect at exactly one point: \\( (3, 5) \\). Their slopes are undefined and zero, respectively, ensuring intersection.

Is there only one point of intersection between two straight lines?

Yes, provided the lines are not parallel or identical. Two distinct non-parallel lines in a plane intersect at exactly one point.

Conclusion

Finding the point of intersection of two lines is more than a classroom exercise—it's a tool used across disciplines to solve spatial, economic, and design challenges. Whether you prefer algebraic precision, visual confirmation, or matrix efficiency, mastering these methods equips you to tackle real-world problems with confidence. Practice each technique, understand when to apply them, and always verify your results.

🚀 Ready to test your skills? Grab two random linear equations, find their intersection using two different methods, and compare results. Share your example in the comments to help others learn!