Why Is A Negative Times A Negative A Positive Explained 2

At first glance, the idea that multiplying two negative numbers results in a positive number seems counterintuitive. After all, how can combining two “negatives” yield something “positive”? This rule, however, isn't arbitrary—it's deeply rooted in consistency, logic, and the structure of arithmetic. Understanding why this works not only demystifies a common stumbling block in math education but also strengthens foundational number sense.

The rule (–a) × (–b) = ab appears early in algebra and persists through advanced mathematics. While students often memorize it for exams, true understanding comes from exploring patterns, real-world models, and mathematical reasoning. This article unpacks the logic behind this principle using multiple perspectives—algebraic patterns, number lines, real-life analogies, and formal proofs—so you can grasp not just *what* happens, but *why*.

1. Pattern Recognition: Building Intuition Through Sequences

One of the most accessible ways to understand negative multiplication is by observing numerical patterns. Let’s examine what happens when we multiply a fixed negative number by a sequence of decreasing integers.

Consider the expression (–3) × n, where n decreases from 4 to –2:

n	(–3) × n
4	–12
3	–9
2	–6
1	–3
0	0
–1	3
–2	6

Notice the pattern: each time n decreases by 1, the product increases by 3. When we reach zero, the result is zero. Continuing the pattern logically, when n becomes –1, we add 3 to 0, resulting in 3. At n = –2, we get 6. There’s no abrupt break in the sequence—the arithmetic remains consistent only if (–3) × (–2) = 6.

Tip: Use pattern-based reasoning to help students predict outcomes before introducing formal rules. This builds number intuition.

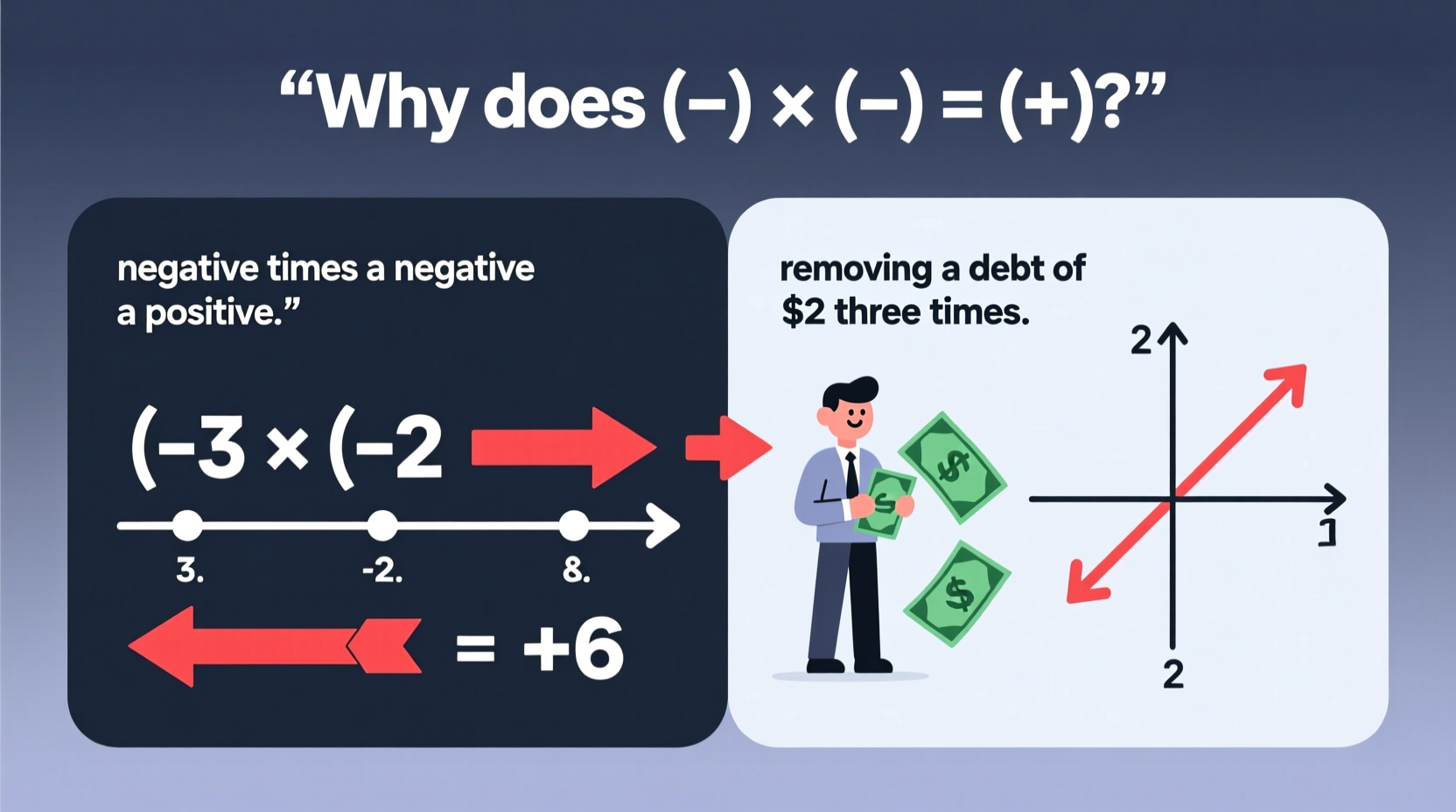
2. The Number Line Model: Visualizing Direction and Reversal

The number line provides a geometric interpretation of multiplication involving negatives. Think of multiplication as repeated addition with directionality.

Multiplying 3 × 4 means moving 3 units to the right, four times—ending at +12. Now consider (–3) × 4: move 3 units to the left, four times—ending at –12. Direction matters.

But what about (–3) × (–4)? If the second negative represents a reversal of direction, then instead of going left 3 units four times, we reverse that action—going right 3 units four times, landing at +12.

In this model, the first number defines the step size and initial direction; the second number controls repetition and whether that direction is flipped. A negative multiplier acts as a \"reversal\" operator. Two reversals cancel out—just like flipping a light switch twice returns it to its original state.

“Multiplication by a negative number is not just scaling—it’s scaling with reflection.” — Dr. Alan Zhou, Mathematics Educator

3. Real-World Analogies: Debt, Time, and Temperature

Abstract rules become clearer when tied to tangible experiences. Here are three practical scenarios that illustrate why a negative times a negative yields a positive.

Debt Cancellation

Imagine you owe $5 per day (–$5/day). Over 3 days, your total debt accumulates to –$15. But suppose we ask: What was your financial position 3 days ago? That is, what is (–5) × (–3)?

Three days ago, you hadn’t yet incurred those daily charges. You were $15 richer than you are now. So (–5) × (–3) = +15. Removing a loss is equivalent to gaining.

Temperature Change

Suppose the temperature drops 2°C per hour (–2°C/hour). In 4 hours, it will be 8°C colder: (–2) × 4 = –8. But what was the temperature 4 hours ago?

Since it has been dropping, 4 hours ago it was 8°C warmer: (–2) × (–4) = +8. Again, reversing a negative change leads to a positive outcome.

Film Reversal Analogy

Think of a video playing backward (negative time) showing a car moving backward (negative velocity). What do you see? The car moves forward. Two reversals produce forward motion—a positive result.

Tip: Use relatable metaphors like debts, time travel, or video playback to make abstract math concepts concrete.

4. Algebraic Consistency: Preserving the Distributive Property

The deepest justification lies in maintaining the consistency of algebraic laws, particularly the distributive property: a(b + c) = ab + ac. If we abandon this rule for negatives, the entire structure of arithmetic collapses.

Let’s test this with an example:

We know that:
(–3) × (5 + (–5)) = (–3) × 0 = 0

Now apply the distributive property:

(–3) × 5 + (–3) × (–5) = –15 + ?

For the sum to equal 0, the missing term must be +15. Therefore, (–3) × (–5) = +15.

This isn’t a coincidence—it’s a necessity. If negative times negative weren’t positive, basic algebra would produce contradictions. The system only holds together if the rule is followed.

Formal Proof Using Additive Inverses

Let a and b be positive real numbers. We want to evaluate (–a) × (–b).

Recall that every number has an additive inverse: a + (–a) = 0.

Consider the expression:
(–a) × (b + (–b)) = (–a) × 0 = 0

By distribution:
(–a) × b + (–a) × (–b) = –ab + (–a)(–b)

For this sum to equal 0, (–a)(–b) must be the additive inverse of –ab—which is +ab.

Therefore: (–a)(–b) = ab

This proof shows the result isn’t a convention imposed by mathematicians—it’s a logical consequence of existing rules.

5. Common Misconceptions and Pitfalls

Despite clear explanations, confusion persists. Here are frequent misunderstandings and how to address them.

• “Two negatives make a positive” applies everywhere. This phrase is misleading. It only holds for multiplication and division, not addition (e.g., –3 + (–5) = –8).
• Negatives are “bad” or “less than nothing.” Framing negatives as deficits or errors leads to conceptual blocks. Instead, treat them as directional values—opposite vectors on a continuum.
• The rule is just memorization. Students who rely solely on rote learning struggle when applying concepts in algebra or physics. Conceptual grounding is essential.

“If we teach math as a set of arbitrary rules, we strip it of meaning. The beauty is in the coherence.” — Maria Chen, STEM Curriculum Developer

FAQ

Does this rule work for all numbers?

Yes. Whether integers, fractions, or decimals, the principle holds: (–x) × (–y) = x × y for all real numbers x and y.

What about negative exponents?

Negative exponents indicate reciprocals (e.g., 2⁻³ = 1/8), not multiplication of negatives. However, if you compute (–2)⁻², it equals 1/(–2)² = 1/4—a positive result because the exponent is even.

Is there a historical reason for this rule?

Early mathematicians like Brahmagupta (7th century India) defined rules for negative numbers in terms of debts and fortunes. The modern formalization emerged in the 18th and 19th centuries as algebra became more abstract and rigorous.

Step-by-Step Guide: Teaching Negative Multiplication

1. Start with patterns. Show sequences like (–4) × 3, (–4) × 2, down to (–4) × (–1) and let learners predict the next value.
2. Use number lines. Demonstrate movement and direction changes with physical gestures or drawings.
3. Introduce real-world models. Apply debt, temperature, or time reversal examples.
4. Reinforce with algebra. Show how breaking the rule breaks the distributive property.
5. Practice with mixed operations. Combine addition, subtraction, and multiplication to reinforce context.

Checklist: Ensuring Student Understanding

• Can explain the rule using at least one real-world analogy
• Can extend a multiplication pattern to predict negative × negative results
• Can distinguish when “two negatives make a positive” applies (only × and ÷)
• Understands that the rule preserves mathematical consistency
• Can solve problems involving multiple negative factors

Conclusion

The rule that a negative times a negative equals a positive is not a quirk of mathematics—it’s a necessary outcome of preserving logical consistency across arithmetic systems. From predictable patterns to real-life analogies and formal proofs, multiple pathways confirm its validity. More than a calculation trick, it reflects a deeper truth: mathematics is a coherent, interconnected framework where rules support and reinforce one another.

💬 Now that you understand the 'why,' how will you explain it to someone else? Share your favorite analogy or teaching method in the comments to help others make sense of this elegant rule.