Why Is M Used For Slope Origins Explanations

In the world of algebra and coordinate geometry, few symbols are as ubiquitous as m when representing the slope of a line. Whether graphing linear equations or analyzing rates of change, students and professionals alike encounter expressions like y = mx + b. But where did this convention come from? Why m, of all letters, was chosen to represent slope has puzzled learners and educators for generations. Unlike many mathematical notations with clear etymological roots, the origin of using m remains surprisingly ambiguous—shrouded in historical gaps, scholarly debate, and occasional myth.

This article explores the leading theories behind the use of m for slope, evaluates historical evidence, and clarifies common misunderstandings about one of mathematics’ most enduring conventions.

The Role of Slope in Mathematics

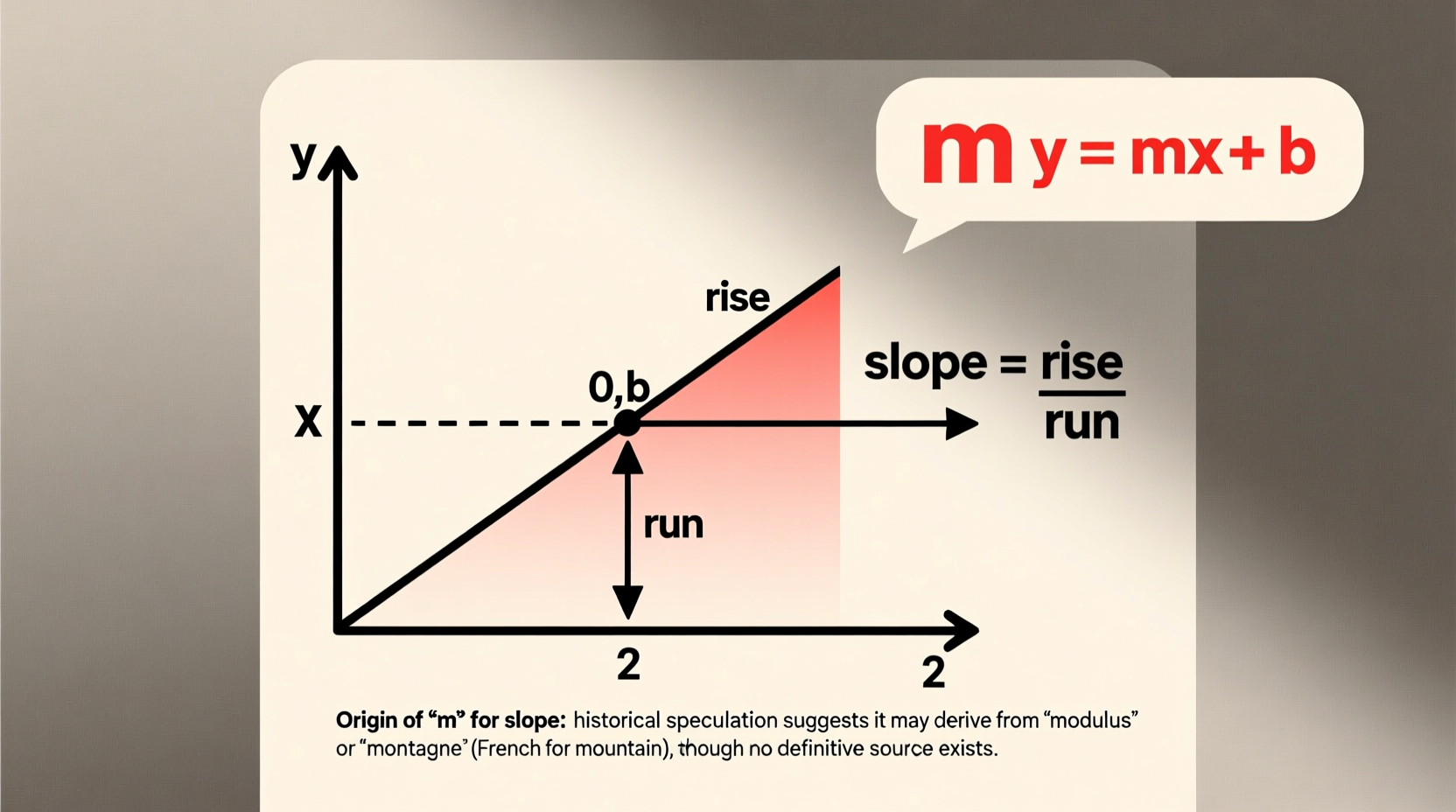
Slope measures the steepness and direction of a straight line on a Cartesian plane. It is defined as the ratio of vertical change (rise) to horizontal change (run) between two points:

slope = rise / run = (y₂ - y₁) / (x₂ - x₁)

In the slope-intercept form of a linear equation, y = mx + b, the coefficient m directly determines how sharply the line ascends or descends. Despite its foundational role, the symbol itself lacks a definitive origin story, making it one of the curious anomalies in mathematical notation.

Historical Theories Behind the Use of 'm'

No single document conclusively explains why m became the standard symbol for slope. However, several plausible theories have emerged over time, each supported by fragments of historical usage and linguistic reasoning.

1. The \"Modulus of Slope\" Theory

One widely cited explanation is that m stands for “modulus of slope.” In 18th and 19th-century mathematical texts, the term *modulus* referred to a factor or constant of proportionality. Vincenzo Riccati, an Italian mathematician, used m in equations involving lines in the 1750s, possibly in reference to a modular value.

Math historian Howard W. Eves noted this possibility in his writings, suggesting that m may have been adopted as shorthand for the modulus governing the inclination of a line. While no direct source explicitly states “m for modulus,” the context fits: early analytical geometry often treated slope as a scaling factor—a kind of modulus relating changes in y to changes in x.

2. French Origins: \"Monter\" or \"Montagne\"

Another popular theory traces m to the French word *monter*, meaning “to climb” or “to rise.” Given that France produced influential mathematicians such as René Descartes and Auguste Comte, it's plausible that French terminology influenced notation.

If slope represents the act of rising, then *m* from *monter* becomes a logical choice. Some also suggest *montagne* (mountain) as a metaphor for incline. However, critics point out that Descartes himself never used m for slope in his original works. The earliest known uses of m appear later in English and German textbooks, weakening the argument for a direct French linguistic link.

3. Arbitrary Alphabetical Assignment

Some historians argue that m was simply an arbitrary letter choice, following a broader trend in mathematics of using middle letters of the alphabet for constants and coefficients. In contrast, variables like x and y occupy the end of the alphabet, while a, b, and c often denote fixed values in equations.

William Emerson, an 18th-century British mathematician, used m in his 1763 work *The Elements of Geometry* when discussing proportional lines. His use wasn’t framed linguistically but rather as part of a sequence of parameters. This supports the idea that m was selected not for meaning, but for consistency within symbolic systems already taking shape.

“Not every mathematical symbol has a deep etymology. Sometimes, convention arises from repetition, not reason.” — Dr. Laura Chen, History of Mathematics Scholar, University of Edinburgh

Global Variations in Slope Notation

Interestingly, m is not universally used. In some countries, different letters represent slope, challenging the assumption that m is a global standard.

Country/Region	Slope Symbol	Common Linear Equation Form
United States, Canada, UK	m	y = mx + b
Germany, Austria	k	y = kx + d
Sweden, Netherlands	k	y = kx + m
Russia, Eastern Europe	k	y = kx + b
France	a	y = ax + b

This variation suggests that the use of m is more cultural than intrinsic. In Germany, k likely comes from *Koeffizient* (coefficient), while in France, a is used as a general parameter. The lack of international consensus reinforces the idea that m gained traction through regional educational practices rather than universal logic.

A Mini Case Study: The Spread of 'm' in American Textbooks

A telling example of how m became entrenched lies in 19th-century American mathematics education. One of the earliest known uses of m in U.S. textbooks appears in Simon Newcomb’s *Elementary Treatise on Coordinate Geometry* (1885). Newcomb, a prominent astronomer and mathematician, used m without explanation, implying it was already recognizable to readers.

By the early 20th century, textbook publishers like McGraw-Hill and Ginn & Company standardized the format y = mx + b across high school curricula. Once adopted at scale, the notation became self-reinforcing: new teachers taught what they had learned, perpetuating the use of m. No formal decree established it—only widespread repetition.

This case illustrates how pedagogical inertia can solidify ambiguous conventions. Even without a documented origin, once a symbol enters mass education, it becomes difficult to displace.

Tip: When teaching slope, acknowledge the mystery of 'm'—it humanizes math and encourages critical thinking about notation.

Common Misconceptions About the Origin of 'm'

Several myths persist about why m is used for slope. While imaginative, they lack historical support.

• Myth: 'm' stands for \"slope\" in Latin (\"gradientem\") – There is no Latin word for slope starting with 'm'. This claim confuses correlation with causation.
• Myth: It honors mathematician M. Dupont or another 'M' namesake – No record exists of a key figure named M. whose work defined slope notation.
• Myth: 'm' means \"measure\" of inclination – While plausible, there is no textual evidence from early mathematicians linking 'm' to \"measure.\"

These stories, though appealing, reflect our desire for neat explanations. The truth may be simpler: someone used m, others copied it, and over time, it stuck.

FAQ

Why do we use 'b' for the y-intercept?

The origin of 'b' is similarly unclear. In the French system, y = ax + b, 'b' may simply follow 'a' alphabetically. In English-speaking countries, it could distinguish the intercept from other constants. Like 'm', its use is largely conventional.

Is there a correct symbol for slope?

There is no inherently \"correct\" symbol. m is standard in many English-speaking countries, but k and a are equally valid elsewhere. The key is consistency within a given context or curriculum.

Could we change the symbol for slope today?

Technically yes, but practically no. Standardization across textbooks, software, and curricula makes shifting symbols extremely difficult. Mathematical notation evolves slowly, if at all, once embedded in education.

Step-by-Step: How to Teach the Concept of Slope Beyond the Symbol

To help students grasp slope beyond memorizing y = mx + b, consider this approach:

1. Start visually: Use graphs to show steep vs. gentle lines, emphasizing rise-over-run.
2. Introduce real-world rates: Connect slope to speed, pricing models, or temperature change.
3. Discuss the symbol’s ambiguity: Explain that 'm' has no definitive origin—this fosters curiosity.
4. Compare global notations: Show how other countries use different letters, reinforcing that symbols are conventions.
5. Encourage notation literacy: Teach students to recognize equivalent forms like y = kx + d or y = ax + b.

💬 Did your teacher ever explain why 'm' is used for slope? Share your experience in the comments and join the conversation on math history and education.

Conclusion

The use of m for slope remains one of mathematics’ charming enigmas. Despite extensive research, no definitive source confirms its origin. Was it “modulus”? A nod to *monter*? Or just alphabetical convenience? The answer may forever lie in the gray area between speculation and tradition.

What matters most is not the letter itself, but the concept it represents—the fundamental idea of rate of change that underpins calculus, physics, economics, and data science. While the mystery of m endures, it serves as a reminder that even in a field governed by logic, human choices and historical accidents shape the way we express ideas.

Understanding the “why” behind symbols enriches learning. It transforms rote memorization into inquiry and invites students to see mathematics not as a rigid set of rules, but as a living language shaped by people, cultures, and time.